

3D成像与机器视觉的实现工具是3D摄像机。在3D成像和机器视觉中相机拍摄所得的图片中除像素坐标与实际物体的坐标存在对应关
系。同时,由于成像原理,最终的图片会发生畸变。实际物体和像素之间的关系由相机内参和外参确定,畸变分径向畸变和切向畸变。
相机标定的任务就是计算出内参,外参和畸变参数。同时利用畸变参数纠正畸变。
展示全部 
张正友标定方法是用于求解相机内参和畸变系数的经典方法。
我们以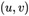 表示像素坐标,以
表示像素坐标,以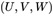 表示世界坐标。张氏标定法利用棋盘格标定板进行标定。
表示世界坐标。张氏标定法利用棋盘格标定板进行标定。

利用相应的图像检测算法可以得到每一个角点的像素坐标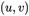 。同时,张正友标定法规定,世界坐标系固定于棋盘格上,则棋盘格上的
。同时,张正友标定法规定,世界坐标系固定于棋盘格上,则棋盘格上的
任意一点 。因此,角点的像素坐标 对应的世界坐标系下的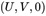 。利用这一关系求解得出相机的内参矩阵,外参矩阵和畸变参数。
。利用这一关系求解得出相机的内参矩阵,外参矩阵和畸变参数。
张正友标定法求解内参矩阵和外参矩阵
先后思路:求解内参矩阵和外参矩阵的积-->求解内参矩阵-->求解外参矩阵。
单点无畸变相机成像模型为:
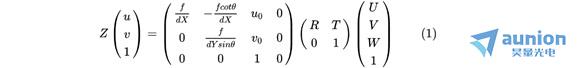
其中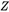 为尺度因子;
为尺度因子; 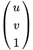 是像素坐标的齐次坐标;
是像素坐标的齐次坐标; 是相机的内参矩阵,包含仿射变换和透视投影;
是相机的内参矩阵,包含仿射变换和透视投影;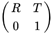 是外参矩阵,包含刚体旋转矩阵
是外参矩阵,包含刚体旋转矩阵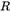 和平移变换矩阵
和平移变换矩阵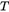 ;
; 是世界坐标的齐次坐标。
是世界坐标的齐次坐标。
因为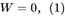 式可简化为:
式可简化为:

其中,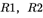 是旋转矩阵
是旋转矩阵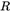 的前两列。同时为了简便将内参矩阵记为
的前两列。同时为了简便将内参矩阵记为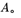
对于不同图片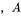 为定值;对于同一张图片
为定值;对于同一张图片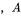 为定值,外参矩阵
为定值,外参矩阵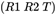 为定值;对于同一张图片上的同一点,
为定值;对于同一张图片上的同一点,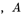 为定值,外参矩阵
为定值,外参矩阵
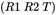 为定值,尺度因子
为定值,尺度因子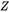 为定值。
为定值。
求解内参矩阵和外参矩阵的积
将内参矩阵和外参矩阵的积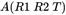 记为 ,根据
记为 ,根据 式,则有:
式,则有:
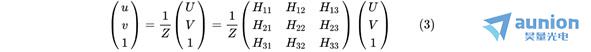
解上式可消去尺度因子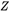 ,得:
,得:
由于尺度因子 已经被消掉,上式对于同一张图片上的角点全部成立。
已经被消掉,上式对于同一张图片上的角点全部成立。
至此,角点像素坐标 和对应的角点世界坐标系下坐标
和对应的角点世界坐标系下坐标 都是已知的。
都是已知的。
当图片标定角点数量大于计算所需时,利用最小二乘法回归最佳的矩阵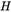 。
。
至此,内参矩阵和外参矩阵的积已经求出。
求解内参矩阵
已知矩阵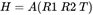 ;同时
;同时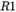 和
和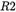 是旋转矩阵的两列,存在单位正交关系。于是有正交约束方程:
是旋转矩阵的两列,存在单位正交关系。于是有正交约束方程:
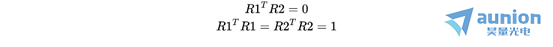
且,由于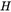 和
和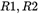 的关系,可知:
的关系,可知:
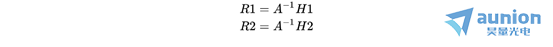
带入可得:
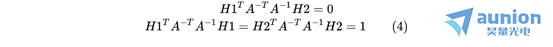
令 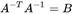 ,则
,则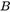 为对称矩阵。可以先求出矩阵
为对称矩阵。可以先求出矩阵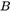 ,再求出内参矩阵
,再求出内参矩阵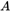 。
。
同时,令:
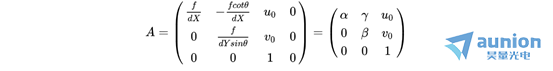
则:
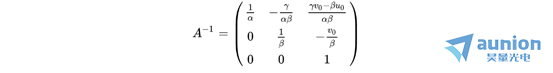
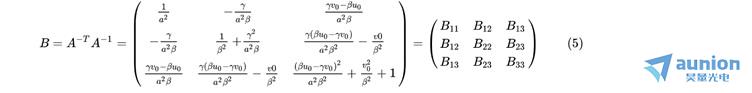
注意:由于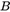 为对称矩阵,部分元素出现了两次。
为对称矩阵,部分元素出现了两次。
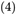 式可化为:
式可化为:
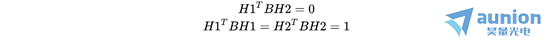
求解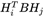 :
:
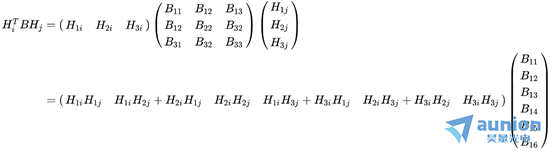
令,
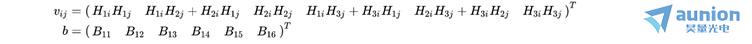
则: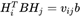 , 式可化为:
, 式可化为:
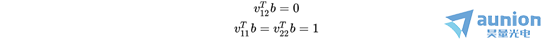
即:
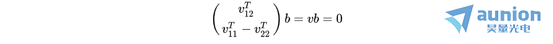
其中,矩阵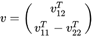 中的所有元素由 的元素构成,且
中的所有元素由 的元素构成,且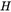 已知,因此
已知,因此 已知。
已知。
此时,我们只要求解出向量 ,即可得到矩阵
,即可得到矩阵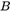 。每张标定板图片可以提供一个
。每张标定板图片可以提供一个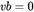 的约束关系,该约束关系含有两个约束方程。但是,向量
的约束关系,该约束关系含有两个约束方程。但是,向量 有6个未知元素。因此,单张图片提供的两个约束方程是不足以解出来向量
有6个未知元素。因此,单张图片提供的两个约束方程是不足以解出来向量 。因此,我们只要取3张标定板照片,得到3个
。因此,我们只要取3张标定板照片,得到3个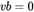 的约束关系,即6个方程,即可求解向量
的约束关系,即6个方程,即可求解向量 。当标定板图片的个数大于3时(事实上一般需要15到20张标定板图片),可采用最小二乘法拟合最佳的向量
。当标定板图片的个数大于3时(事实上一般需要15到20张标定板图片),可采用最小二乘法拟合最佳的向量 ,并得到矩阵
,并得到矩阵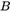 。
。
根据 式中的矩阵
式中的矩阵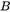 的元素和相机内参
的元素和相机内参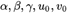 的对应关系,可以得到:
的对应关系,可以得到:
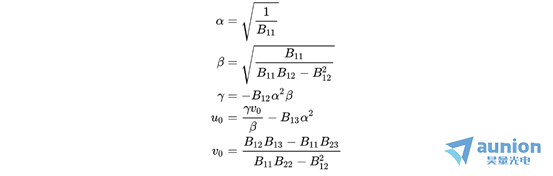
可以得出相机的内参矩阵:
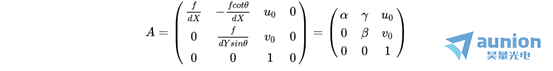
求解外参矩阵
已知: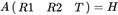 ;同时,我们已经求解得到了矩阵
;同时,我们已经求解得到了矩阵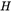 (对于同一张图片相同,对于不同的图片不同)、矩阵
(对于同一张图片相同,对于不同的图片不同)、矩阵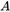 (对于不同的图片
(对于不同的图片
都相同)。通过公式: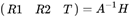 ,即可求得每一张图片对应的外参矩阵。
,即可求得每一张图片对应的外参矩阵。