

什么是快速傅里叶变换?
快速傅里叶变换
模拟信号使用傅里叶变化公式,数字信号可以采用离散傅里叶变化公式,但是离散傅里叶变化公式计算量大,所以对于离散的信号,现
在都是采用快速傅里叶变化(Fast Fourier Transformation)
这里以一个随机信号表示离散的信号

依据上述公式,如果计算X(k),乘法计算8(num)次,加法计算7(num-1)次,计算所有的频谱,需要乘法64(num^2)次,加
法计算56(num×(num-1))次。假设乘法使用四个时间周期T,加法使用一个时间周期T,那么8个数据占据的周期大约是312T
将这个公式和一些软件计算的结果进行对比,结果是一样的

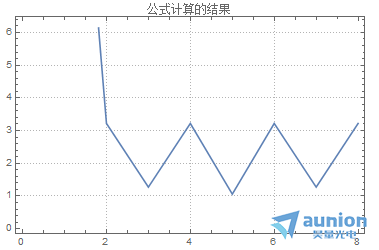

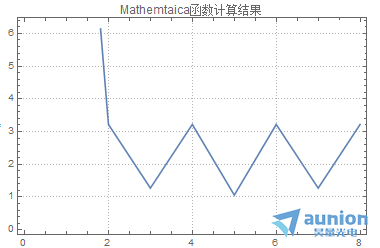
FFT
下述公式,首先将系数奇数项和偶数项分开,然后偶数想提出公因式e^(-I 2π/N k),保持两个多项式的e指数有相同的形式,最后合并
2和N,奇数和偶数项构成新的多项式。
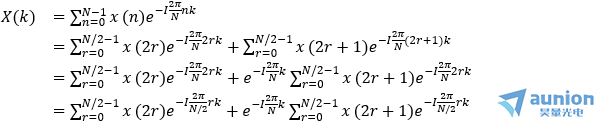
假设序列的长度为8,按照上述规则,将序列按照奇偶不断的分裂,直到最后
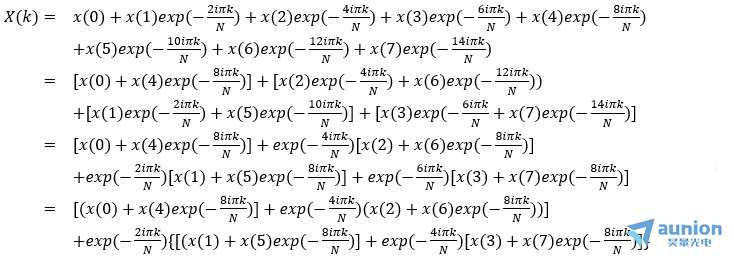
观察最后一个等号后的公式,从小括号,到中括号,到大括号,每个括号作为一层,可以得到网上的蜘蛛图
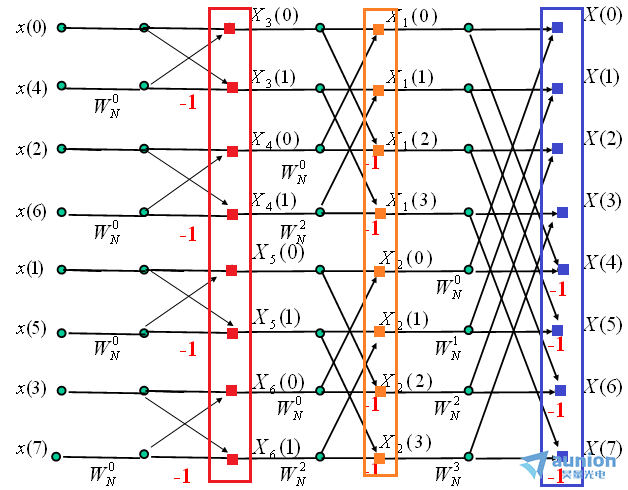
首先从小括号看起,小括号内x0,x2,x4,x6没有系数,而x1,x3,x5,x7的系数是exp(-8iπk/N),k从0到7内取任何整数,exp(-8iπk/N)无
非是+1或者是-1,所以看到在x1,x3,x5,x7后面可能跟随着两个系数W_N^0或者-1,就是表示相乘的意思,然后在红色方框内相遇
,相遇代表相加。他们是第一层,同时作为下一层的输入。下一层输入的系数是exp(-8iπk/N),k从0到7改变,系数可出现四种,
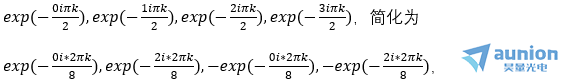
按照图上的表示应该是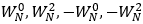 ,同时它也作为第二层结果,同理可以得到第三层结构。每一层结构有8个数据,每个数据
,同时它也作为第二层结果,同理可以得到第三层结构。每一层结构有8个数据,每个数据
都结构都是做了一次乘法和一次加减法。相对于DFT而言,DFT做乘法64次,而这里做的乘法只有不到8*lg8,也就是大约24次左右
,因此能够节省很多时间。
上面的叉形图中,最后的数字排列也是存在规律的。
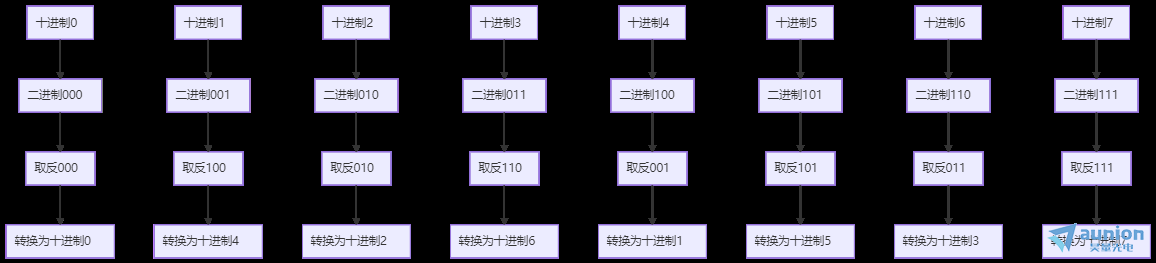
二维傅里叶变化FFT2是对一个二维矩阵,先做一次FFT,然后转置后再做一次FFT。这里以一个实际的例子作为参考,输入的信号是一个3*3的矩阵
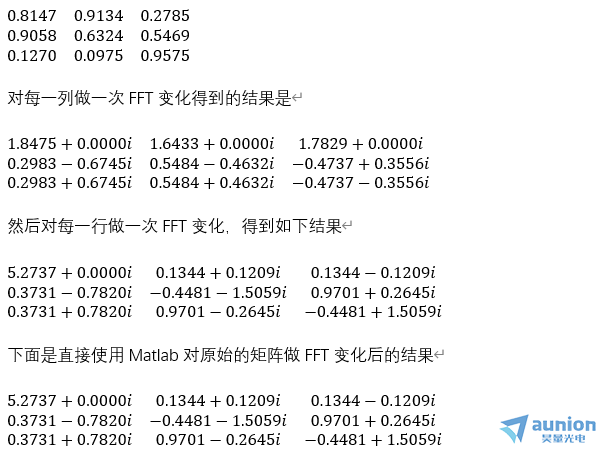
如果用matlab表示信号x,两次FFT变化可以写为fft(fft(x),3,2),一次FFT变化可以记作fft2(x)
您可以通过我们的官方网站了解更多的产品信息,或直接来电咨询4006-888-532。
展示全部 
展示全部 
