拉普拉斯变换
拉普拉斯变换
傅里叶变换
傅里叶变换需要满足狄利克雷条件：
1. 在一个周期内，连续或只有有限个第1类间断点
2. 子一个周期内，极大值和ji小值的数目应是有限个
3. 在一周期内，信号是绝对可积的
补充：间断点分为两类：
1. 第1类不连续点：
可去不连续点：不连续点两侧函数的极限都存在，且相等
跳跃不连续点：不连续点两侧函数的极限存在，但不相等
2. 第二类不连续点：
无穷间断点：左右两点中，至少存在一个点的极限为无穷
振荡间断点：函数在该点没有定义，一直在变换。例如y=sin(1/x)在零点位置
对于狄拉克雷条件，很多函数无法满足，例如e指数，抛物线等等。因此拉普拉斯在傅里叶变换的条件上添加一个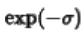
进行衰减，当t大于0的时候，整个函数都是快速衰减的，t<0的范围并不是关心的重点，所以将他们都置为零处理。所以在傅里叶变换的基础上，生成一个更加泛化的变换公式
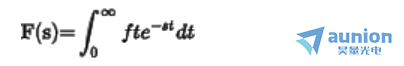
其中
，当
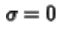的时候，傅里叶变换。拉普拉斯变换使用符
表示。
拉普拉斯变换
1. 时域和频率区别
从时域观察，傅里叶变换中的某个频率，他是边长为1的单位圆圈。但是拉普拉斯变换，他是一个不断衰减的圆。
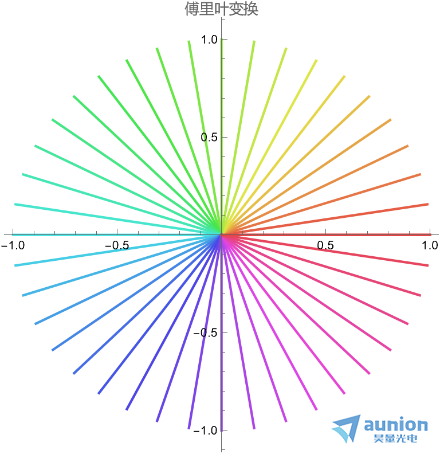
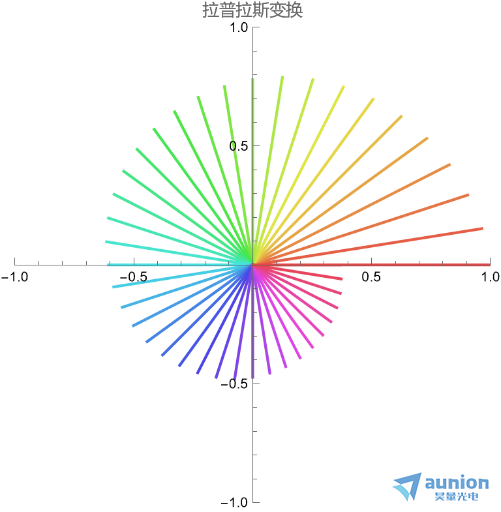
从频域看，傅里叶变换是一维的，拉普拉斯变换是二维的
例如几个正弦函数组成的波形，傅里叶表达式如下
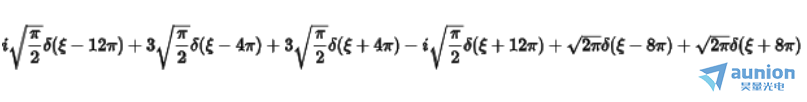
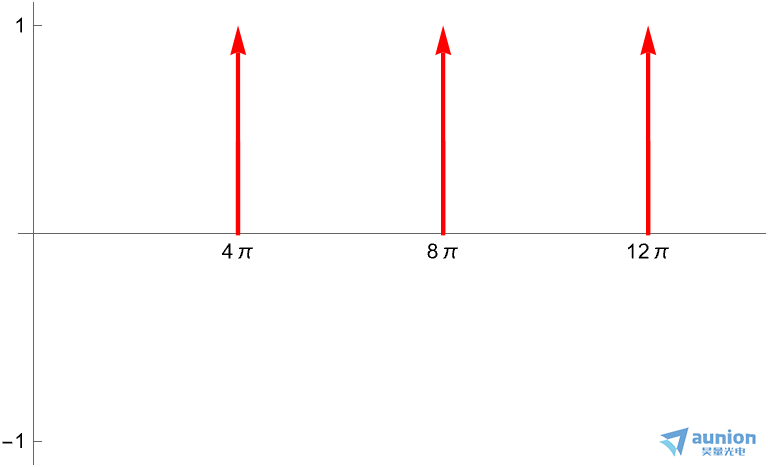
拉普拉斯的表达式是为
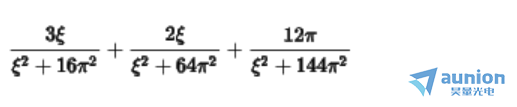
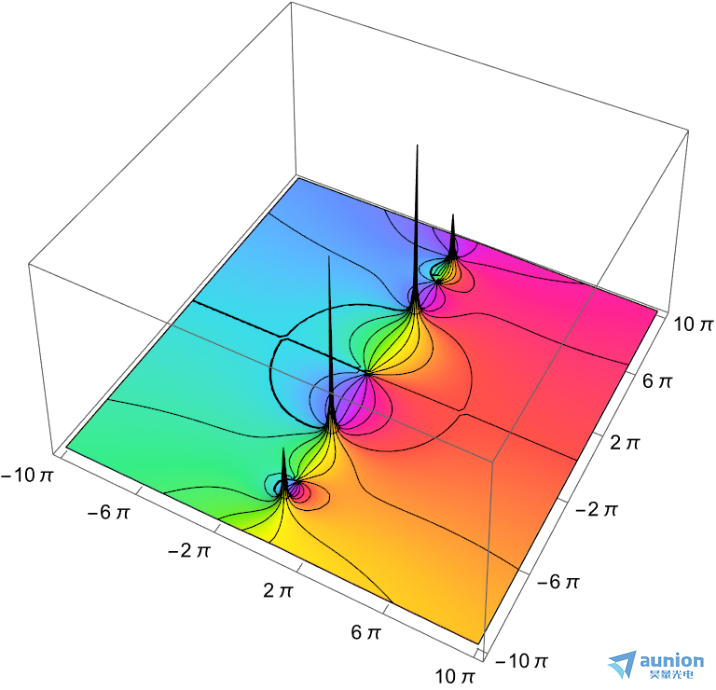
可以从下图中看出，在不同的位置，代表的形状也是不同的。当处于坐标轴左侧是，是区域稳定的；当处于纵轴的情况下，产生恒定的振荡；处于右侧情况下，振动趋于不稳定。
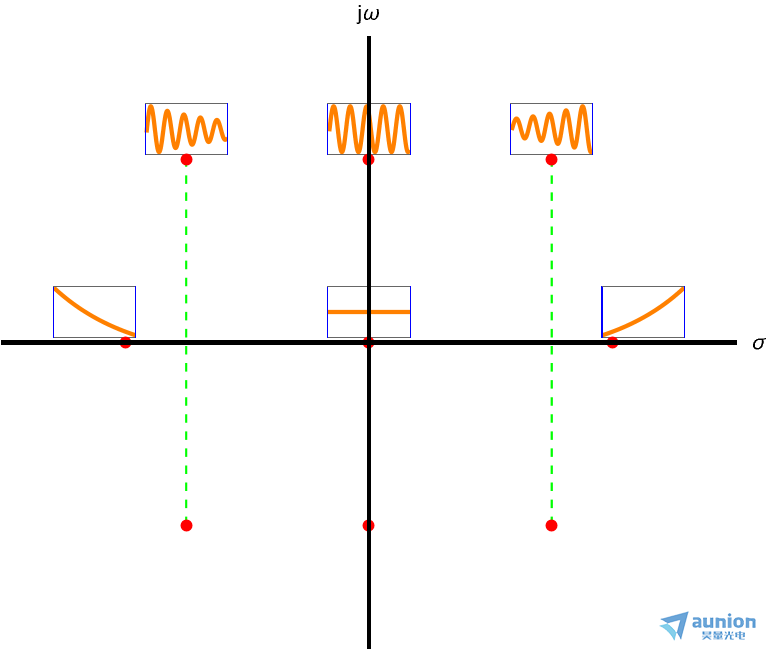
2. 收敛条件
当坐标趋向于无穷远的的时候，幅值趋向于零
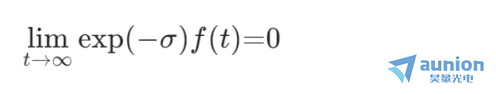
即满足上述关系的时候，整体收区域收敛的，因此只要找到合适的
便能找到找到收敛区域
3. 零点和ji点
拉普拉斯构成的传递函数，存在的分子和分母两项。当分子为零时的解为零点，当分母为零时的解为ji点。
关于昊量光电：
上海昊量光电设备有限公司是光电产品专业代理商，产品包括各类激光器、光电调制器、光学测量设备、光学元件等，涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532。
展示全部 
