

变换
变换
相量变换
一个角频率为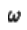 的正弦波,可以表示为
的正弦波,可以表示为
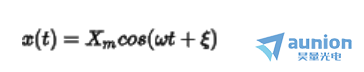
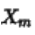 是振幅,
是振幅,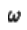 是角频率,
是角频率,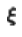 是相位,角频率可以表示为
是相位,角频率可以表示为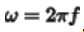 ,单位是
,单位是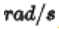 。
。
上述表达式复数的形式描述为
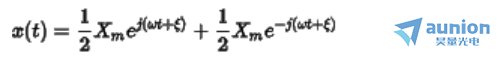
令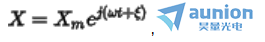 ,称
,称 为正弦波的相量
为正弦波的相量
相量到正弦波的变换称为相量变换
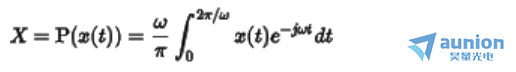
反过来称为相量反变换

其中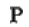 称为算子。如果对原始信号乘以一个微分算子
称为算子。如果对原始信号乘以一个微分算子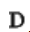 ,然后进行相量变换,可以得到性质
,然后进行相量变换,可以得到性质
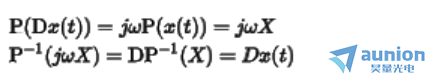
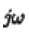 常称为激励的复数频率,后面用
常称为激励的复数频率,后面用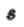 表示
表示
连续时间LTI系统相量变换
对于一个连续时间系统描述为
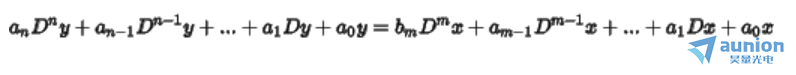
根据上述的性质,对两边同时乘以一个相量变换算子,zui终得到
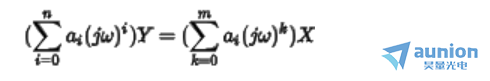
或者以一种更见紧凑的方式进行描述得到
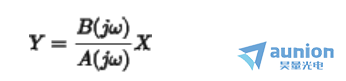
正弦信号响应
假设输入信号为固定频率的正弦信号
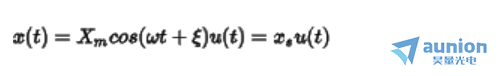
求解系统的完全响应分为零输入响应(齐次解)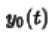 和零状态响应(特解)
和零状态响应(特解) ,所以zui终响应可以表示为
,所以zui终响应可以表示为
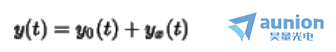
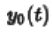 是当输入信号都为零的条件下求得的解,即
是当输入信号都为零的条件下求得的解,即
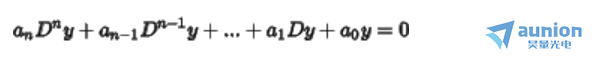
解的形式多为
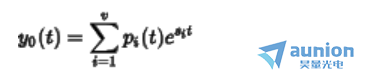
其中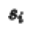 称为系统的固有频率,根据之前的讨论,[MISSING IMAGE: , ]在一个复数坐标中,当在坐标系的左半边的平面内是,随着
称为系统的固有频率,根据之前的讨论,[MISSING IMAGE: , ]在一个复数坐标中,当在坐标系的左半边的平面内是,随着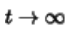 时信号也趋于零,因此该系统渐进稳定的,如果有一个或者多个频率位于右边,则称系统非稳定的。
时信号也趋于零,因此该系统渐进稳定的,如果有一个或者多个频率位于右边,则称系统非稳定的。
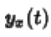 是系统处于零状态下,给一个信号是的响应。因为不关心时间小于零的部分,所以输入和输出信号都是和一个单位阶跃信号的乘积
是系统处于零状态下,给一个信号是的响应。因为不关心时间小于零的部分,所以输入和输出信号都是和一个单位阶跃信号的乘积
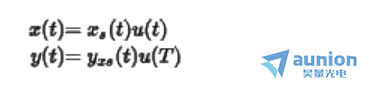
将上述返程同样带入线性方程组中,同样也需要分成其次和非齐次。因此zui终的完全响应可描述为
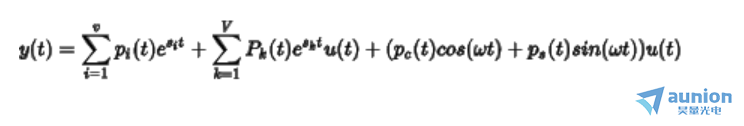
非正弦信号响应
上述情况中,激励信号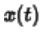 是单一频率,但是多数情况下,输入信号包含多个频率。假设任意输入的信号频率包含
是单一频率,但是多数情况下,输入信号包含多个频率。假设任意输入的信号频率包含 ,任意一个信号可以描述为
,任意一个信号可以描述为
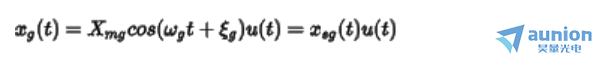
根据上述的计算,在非正弦情况下完全响应也同样是零输入响应和零状态响应之和。因此描述为
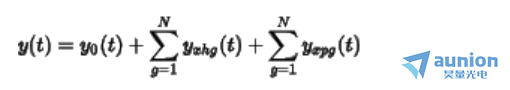
 表示齐次解,
表示齐次解, 表示特解
表示特解
转移函数和频率响应
线性方程中包含微积分的信息,但是通过相量变换可以将微分方程转换为代数方程。定义转移函数(也称为频率响应)为
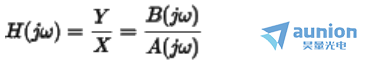
根据公式幅频和相位响应定义为
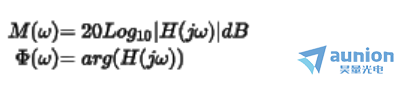
将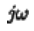 记作
记作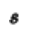
当转移函数的分子部分为零是的根,称为零点
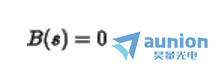
零点用符号
当转移函数的分母部分为零的根,称为ji点
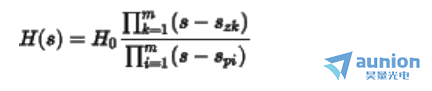
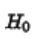 称为尺度因子。每个ji点定义为
称为尺度因子。每个ji点定义为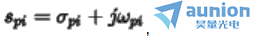 ,定义ji点的模
,定义ji点的模
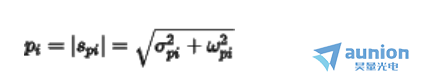
同时定义品质因数
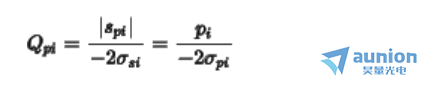
关于昊量光电:
上海昊量光电设备有限公司是光电产品专业代理商,产品包括各类激光器、光电调制器、光学测量设备、光学元件等,涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等;可为客户提供完整的设备安装,培训,硬件开发,软件开发,系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息,或直接来电咨询4006-888-532。
展示全部 
