梯度消失问题
梯度消失问题
假设输入层784个，输出参数10个，每一个隐藏层包含30个元素。
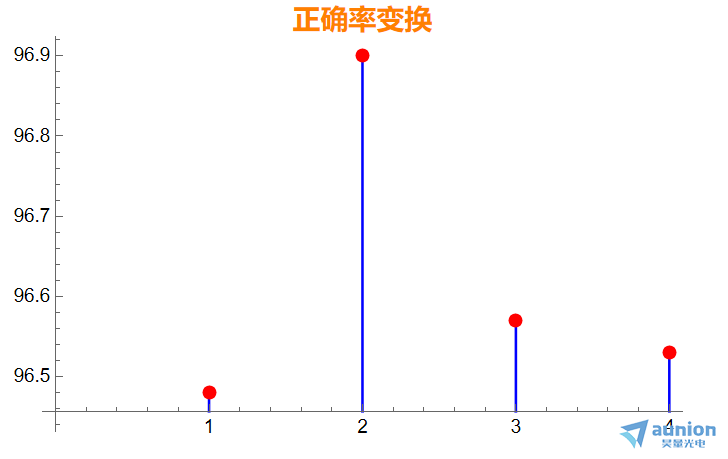
1. 当隐藏层为一层，正确率为96.48%
2. 当隐藏层为二层，正确率为96.90%
3. 当隐藏层为三层，正确率为96.57%
4. 当隐藏仓为四层，正确率为96.53%
增加隐藏层，并没有提高正确率，反而有时会减小。
做一个简单的假设，输入层只有一个参数，包含四个隐藏层，输出也只有一个。
x表示输入参量，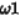
表示权重（是一个向量），b1表示偏置，
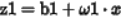。每个隐藏层输出为
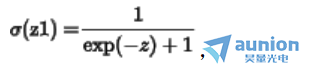，即每个隐藏层的输出结果，使用a描述，通常用z小二乘的方式描述评价函数C，梯度下降的方法不断修改其中的参数
和参数b，令评价函数C趋向于Min，此时神经网络描述的函数既是想输入函数拟合的过程。
如果此时去求解评价函数C对于偏置b1的导数，用到导数的链式法则。
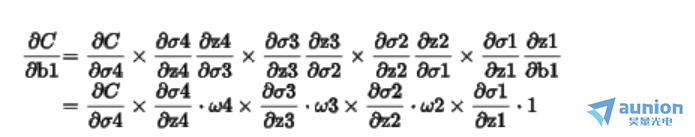
一般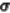
的导数如图所示
如上图所示，通常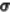
的导数，Max值为0.25。
如果乘以
后模值小于1，那么原靠近输入的层的梯度越小，这就是导致梯度消失的原因
当然也有可能是乘以[MISSING IMAGE: , ]后大于1的情况存在，那么越靠近输入层的梯度越来越大，这就是导致梯度爆炸的原因。
当隐藏层数量过多的时候，可能会导致梯度消失或者梯度爆炸，zui终令神经网络变得不稳定。
假设需要输入函数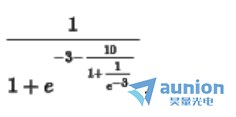
，在区间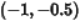
之间输入和输出如图所示
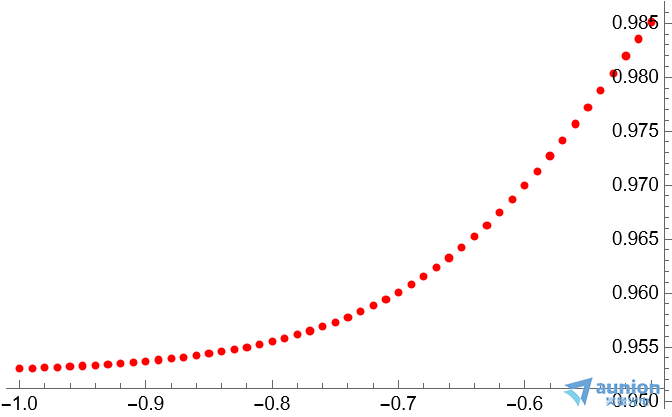
此时假设设计一个神经网络，
输入神经元为1个，输入数据为其横坐标；
输出神经元为1个，输出数据来自于纵坐标；
学习率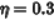
；正则化表达式
；
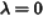隐藏层有2个，每层为2个神经元
大致结果如下图所示
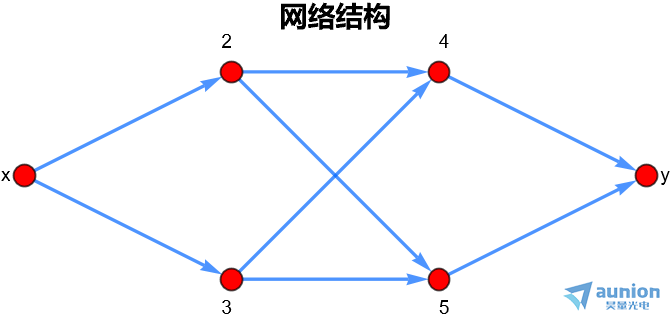
通过梯度下降的方法，计算每一层的权重和偏置
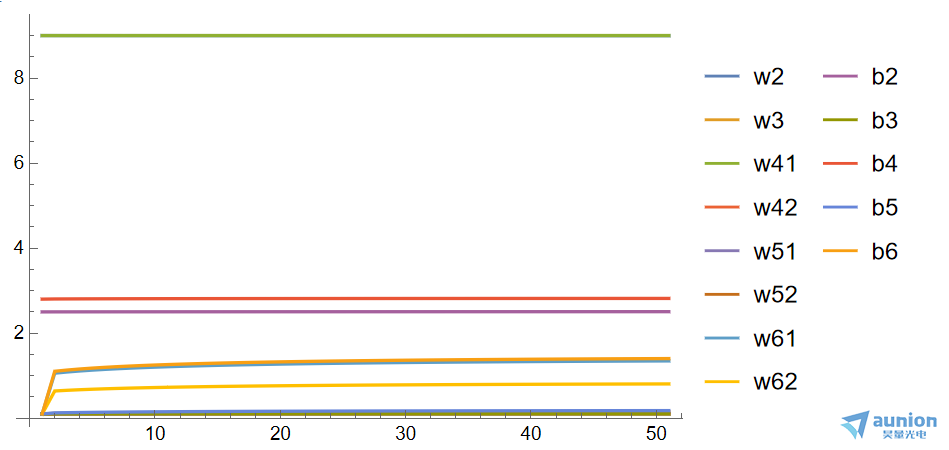
不同初始值会收敛在不同的极值，虽然已经将初始值的位置靠近与真实情况，虽然收敛但是仍旧收敛在附近的位置。
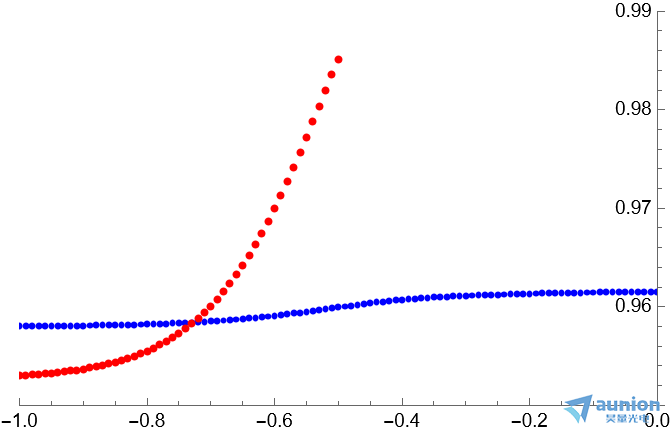
上述红点表示原始数据，蓝色是拟合参数后的结果，因为拟合稳定后只是收敛在附近的位置，所以无法正确的计算正确的结果。
每一层输出的稳定性定义：将每一层迭代前的结果，和迭代后的结果相减，取2范数作为稳定性的z终评价。以迭代次数作为横坐标，每一层的稳定性指标作为纵坐标，每一层形成一根曲线。仍旧是以上述的结构作为基础，观察第1层隐藏层、第2层隐藏层，输出层的结果。取特定位置x=-0.7，隐藏层1和隐藏层2，以及输出层的结果如下图所示
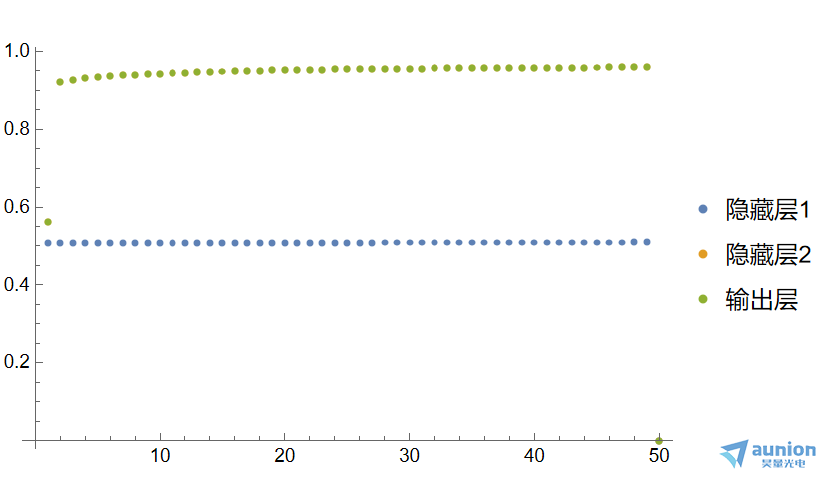
他们的差分结果可以表示其梯度变换
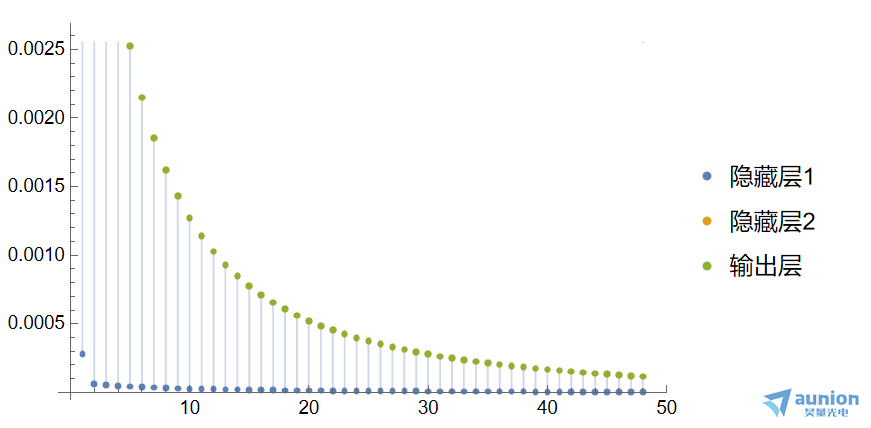
这个恰好对应于当初的公式，不同的输出层的学习率是不同的，而且大致保持这一定的关系。正是这种关系，有可能导致梯度消失或者梯度爆炸的缘故。
关于昊量光电：
上海昊量光电设备有限公司是光电产品专业代理商，产品包括各类激光器、光电调制器、光学测量设备、光学元件等，涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532。
展示全部 
