正则化过拟合
正则化过拟合
假设由一个二次函数产生的信号x^2/10+2 x+1，其中包含了一些噪声
对应波形如图所示
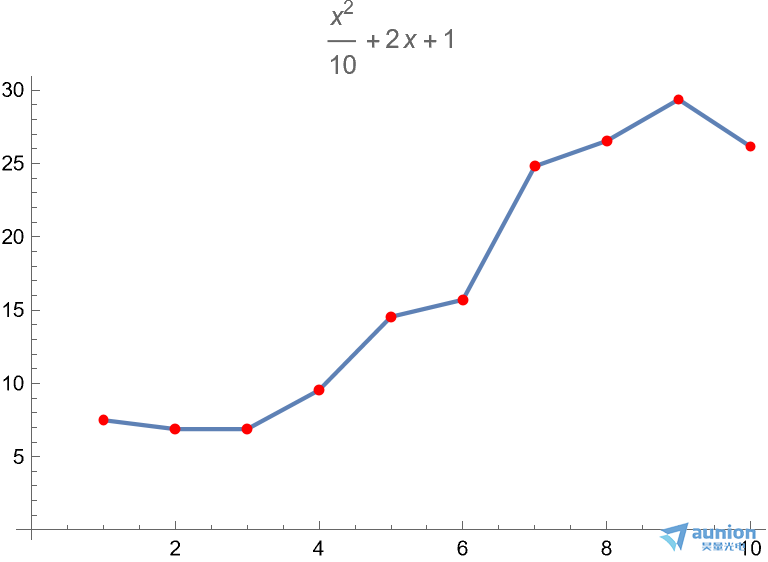
不了解函数的具体波形的情况下，使用不同阶数去拟合函数的波形，分别获得
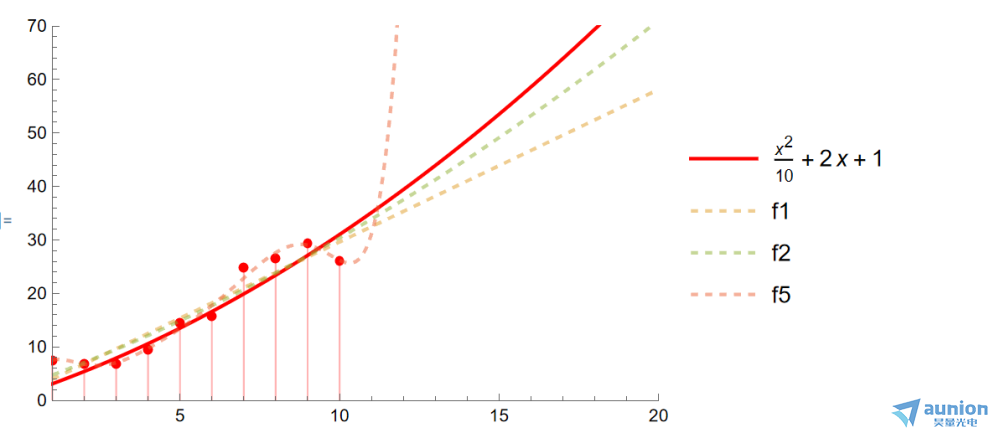
当拟合的参数过少，属于欠拟合。当引入过多高阶项时，虽然当时误差见笑了。但是如果继续添加新的数据，误差却是越来越大。为了抑制高阶项的系数，引入正则化的方法，将高阶的系数保持在一定的范围内。
例如一个函数
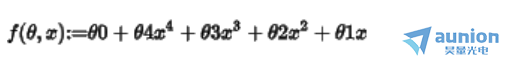
对上述公式进行正则化处理，正则化可以分为L1正则化和L2正则化。
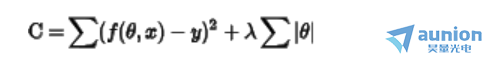
或者
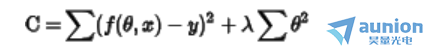
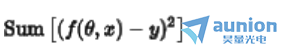通过zui小二乘法计算的代价函数，
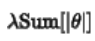为L1正则化，
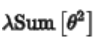为L2正则化。
假设以L2正则化为例，对C进行求导，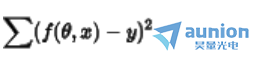
仍旧保持不变，梯度仍旧区域原来的位置，但是
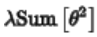求导后得到
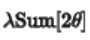，他的梯度位于原点位置，因此整体会将参数
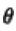拉向远点位置，当
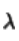越大，就越偏向于远点，从而减小这几项系数的权重。因此
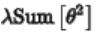因为称为惩罚项。
以一个简单方程为例
假设代价函数为x^2 - 6 x + 1 + y^2 - 6 y + 1 + 0.5 x y
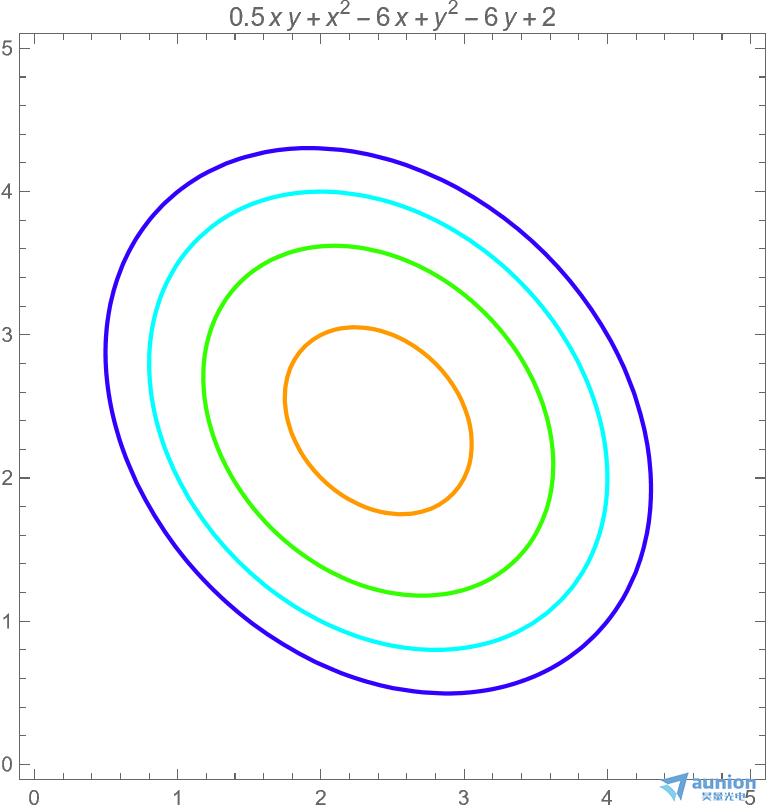
如果仍旧是按照梯度下降算法去计算，那么zui低点位于{2.4, 2.4}
如果加上惩罚函数后，随着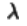
不断增加，代价函数Min值zui终会更加靠近原点
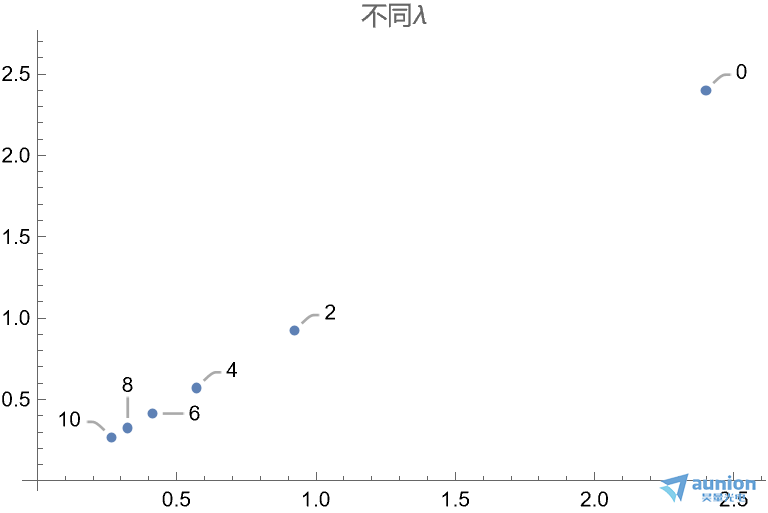
将Signal信号为例子，抑制高阶参数
L2正则化公式可以按照下述方式描述，本身是为了求解几个系数。然后根据梯度下降算法求解Min值
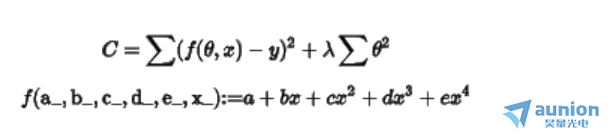
正确的方程加应该是a->1, b->2, c->0.1, d->0, e->0。当没有L2正则化的情况下，常规的评价函数获取的解如下
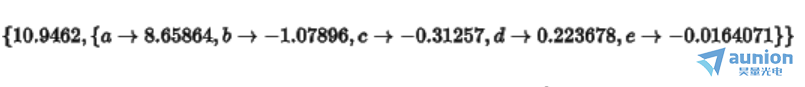
当添加L2正则化后，需要惩罚的系数为c和d。不同参数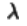
的情况下得到。不断增大[MISSING IMAGE: , ]的情况下，d和e越来越趋近于零
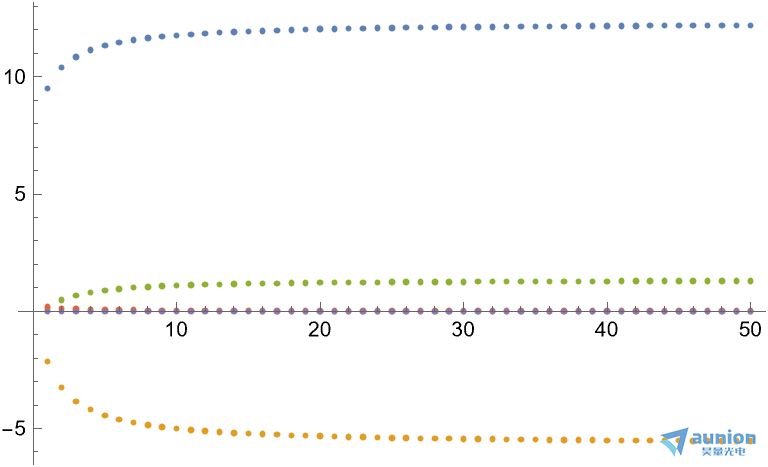
zui终结果是
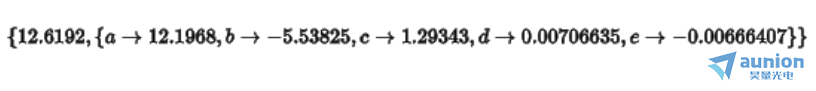
与初始值
像差还是非常远的
增加采样数据点数
将原有的信号从10个变成30个点
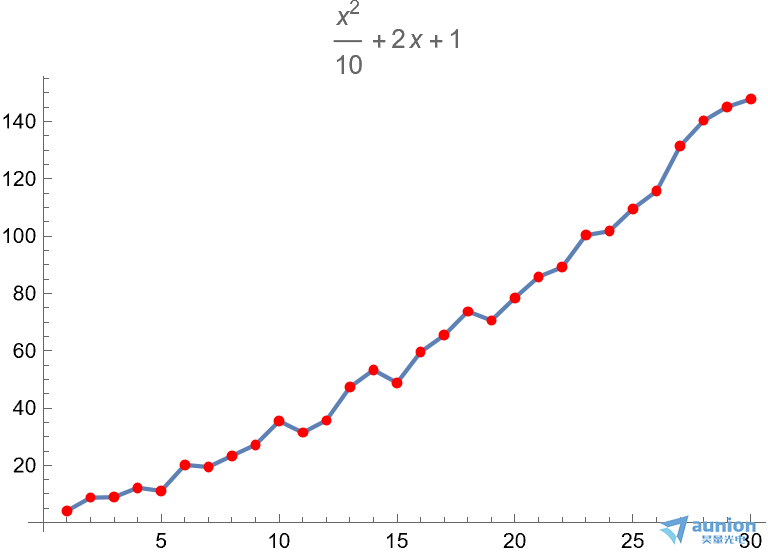
同样使用梯度算法，并且不断增加系数的大小
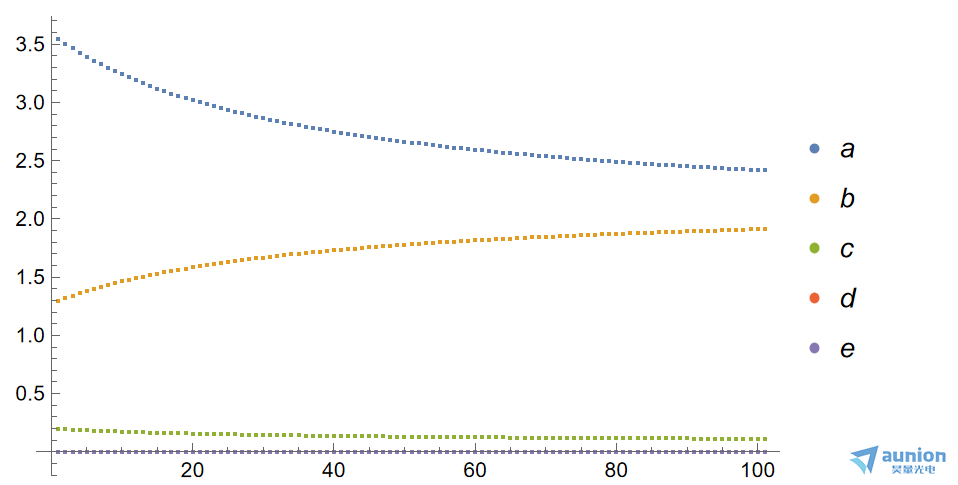
五个系数从zui初的
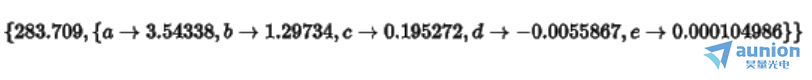
变成
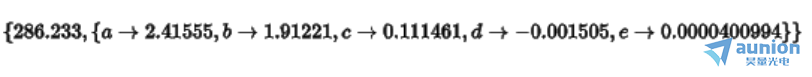
可以看到他的确一边压制高阶项，同时低阶项目也越来越准确。
了解更多详情，请访问上海昊量光电的官方网页：
https://www.auniontech.com/three-level-46.html
更多详情请联系昊量光电/欢迎直接联系昊量光电
关于昊量光电：
上海昊量光电设备有限公司是光电产品专业代理商，产品包括各类激光器、光电调制器、光学测量设备、光学元件等，涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532。
展示全部 
