卷积核
卷积核
函数滤波，除了在傅里叶平面的滤波外，还可以采用卷积的方法进行滤波。这里以高斯函数为例，对信号滤波，高斯函数形式为
其中
指代方差当
=1时，函数的的傅里叶变化结果为
若高斯函数采样点数为3， 其傅里叶变换后的公式为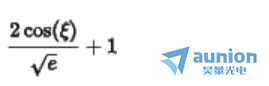
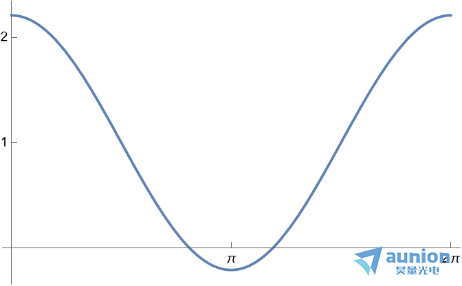
若高斯函数采样点数为5， 其傅里叶变换公式为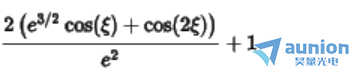
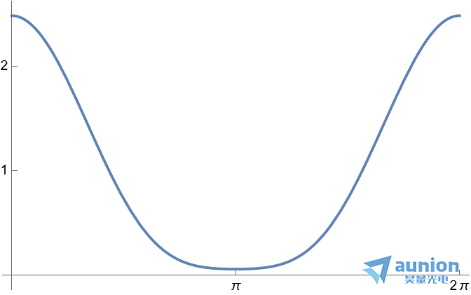
若高斯函数采样点数为7，其傅里叶变换公式为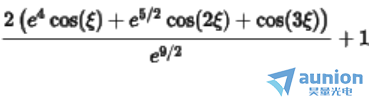
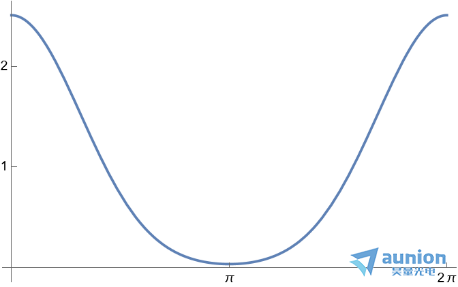
当
=4时，函数的的傅里叶变化结果为
若高斯函数采样点数为3， 其傅里叶变换后的公式为
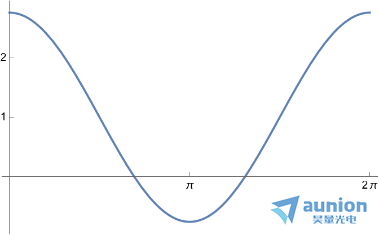
若高斯函数采样点数为5， 其傅里叶变换公式为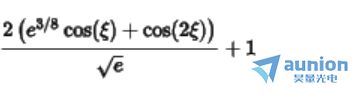
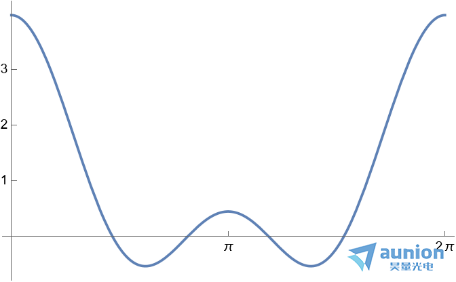
若高斯函数采样点数为7，其傅里叶变换公式为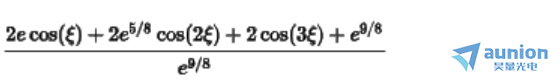
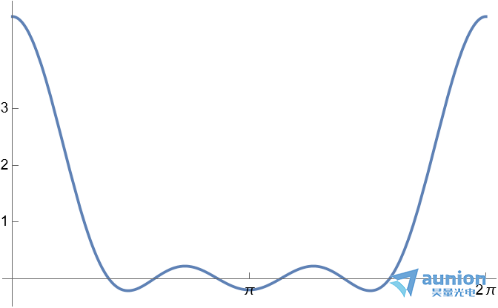
上述两个例子，一个时增加高斯函数的采样宽度，即卷积核的大小，可以令低通滤波器迅速下降，增加
会减小低通滤波器的带宽。
上述例子横轴取值范围时保持在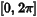
之间，如果将范围进一步口中到[-6\[Pi], 6\[Pi]]之间，并且仍旧时以
=1作为例子，采样点数为3
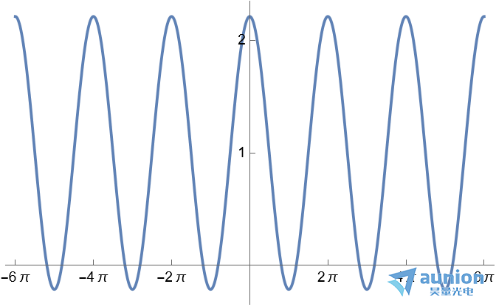
从曲线可以看出，高频信号是没有截至的。因此认为，如果使用这种类型的高斯低通滤波器，可以改善吉布斯的效应。
例子1- 正弦信号
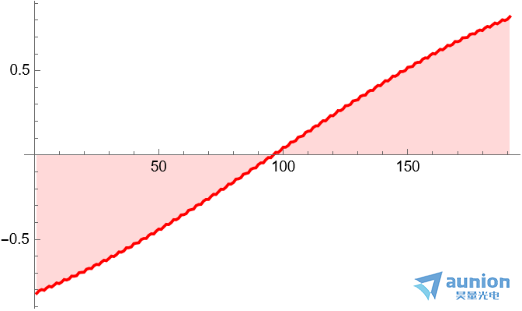
信号采用两个正弦信号叠加而成，其中一个是低频正弦，另一个是高频正弦。通过低通滤波器后，低频信号可以被保留，高频信号被抑制。信号长度为201， 对其傅里叶区间做滤波，滤波区间令61~141的值都为零
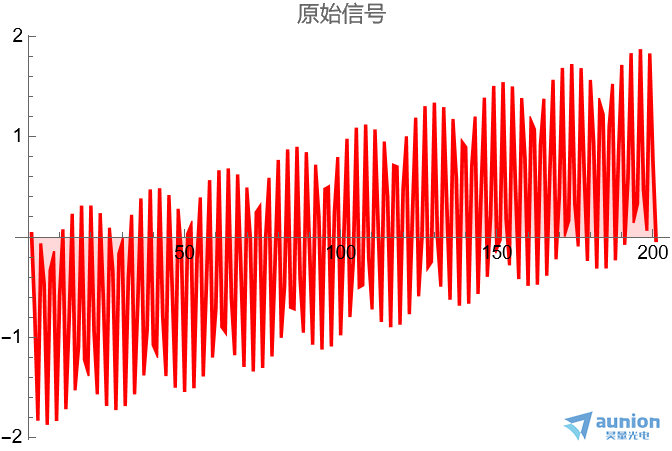
经过滤波后，信号两端因为吉布斯现象，出现明显的振铃。
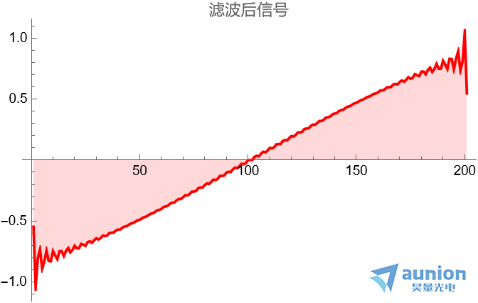
如果采用高斯低通滤波器，构建一个类似的低通滤波器，卷积核大小为11， 方差设置为2.5，得到的滤波器形状为
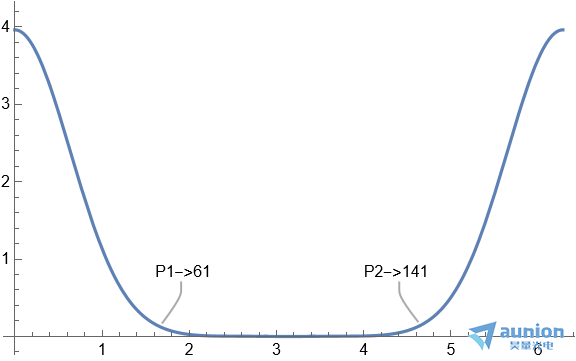
经过低通滤波器后的波形为
例子2-矩形
因为上述例子可能并不是特别明显，使用一个矩形作为例子，信号波形如图所示
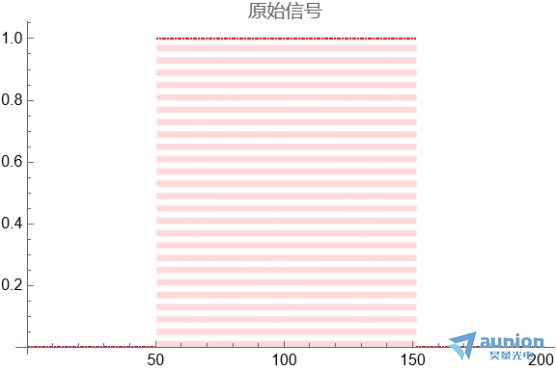
同样是将傅里叶区间61~141个像素置零后，作为一个低通滤波器，得到的信号在边沿还是有明显的吉布斯现象
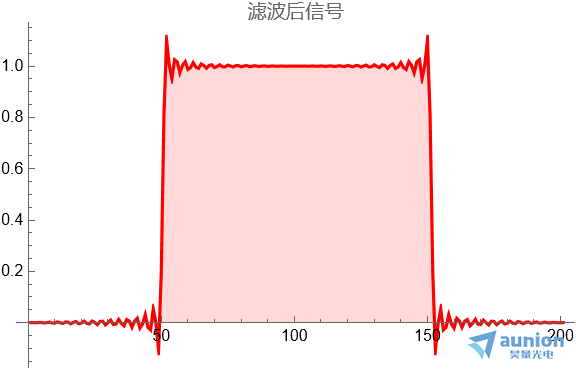
如果采用卷积的方式，在傅里叶频谱范围内滤除了高频信号，但是在傅里叶区间的范围外的高频信号却能够保留。
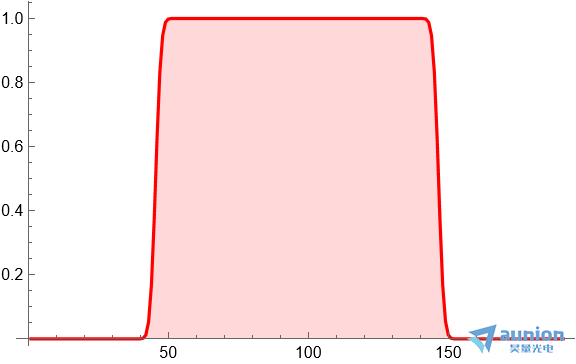
关于昊量光电：
上海昊量光电设备有限公司是光电产品专业代理商，产品包括各类激光器、光电调制器、光学测量设备、光学元件等，涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532。
展示全部 
