

GS算法(Gerchberg-Saxton algorithm)是一种迭代方法,当输入和输出端的各自光强分布已知时,可以通过光学传播函数,例如
傅里叶变化,来恢复光束的相位分布。
一束激光可以分为两部分,一部分是相位,另一部分是光斑光强分布,他们是相互关联的,可以通过改变光束的相位部分,对光斑进行
整形。上述GS算法就是其中的一种方法。
主要分为四步
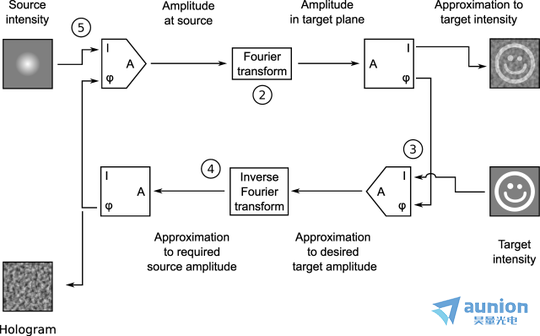
1.假设入射光斑是均匀光强,相位因为是未知的,可以用一个随机相位替代,或者通过Target Intensity的IFFT变化求得
2.然后经过FFT变化后,得到的是焦距是的光斑分布,光强与Target Intensity比较近似,但是不够理想
3.替换上述步骤的光强分布,保留相位分布,得到新的一束激光
4.经过IFFT变化后保留光斑的相位,作为下一次迭代的初始相位
通过上述步骤的反复迭代,会不断改善Approximation to target intensity的光斑。
Matlab代码参考:
%% 数据初始化
pic = 'test.jpg'; % 输入图片
file = 'phase.bmp'; % 图片保存位置
num = 1000; % GS迭代次数
%% 读取图片
im = imread(pic);
im = rgb2gray(im);
im = im2double(im);
%% GS算法
im = mat2gray(im);
light = gpuArray(im); % 加入CUDA,提高计算速度
light = ifft2(light); % 计算初始相位
for n = 1:num
phase = angle(light);
light = 1.*exp(1i*phase); % 1. 均匀光强入射光
light = fft2(light); % 2. 聚焦面上的光强
phase = angle(light);
light = im.*exp(1i*phase); % 3. 理想光斑替换
light = ifft2(light); % 4. 傅里叶逆运算
end
% 均匀光入射后再做一次傅里叶变化
phase = angle(light);
light = 1.*exp(1i*phase);
light = fft2(light);
intensity = mat2gray(abs(light));
imshow(intensity);
%% 保存相位图
phase = gather(phase); % 将phase返回到内存中
imwrite(mat2gray(phase), file)
备注:
1. CUDA可以提高运算的速度,例如上述过程,当上述1000此循环,没有CUDA的时候,循环过程保持在8秒以上,当启用CUDA后,一般在1.1秒左右。
2. 随着迭代次数的增加,恢复后的光强越来越清晰

3.通过对比原始图和经过迭代后的图片,可以判断观察后图片的恢复程度

您可以通过我们的官方网站了解更多的产品信息,或直接来电咨询4006-888-532。
展示全部 
展示全部 
