

哈特曼传感器波前重建模拟,哈特曼传感器是在相机前放置一个微透镜阵列组成。光束经过每个微透镜后都会聚焦在一点,聚焦点的位
置被能够反应出光束的方向,然后反推出光的波前信息。下面的内容是模拟光束经过透镜后聚焦的过程,然后简单的叙述了两种相位恢
复的算法。
关于哈特曼传感器的原理的介绍及相位恢复方法
哈特曼传感器是在相机前放置一个微透镜阵列组成。光束经过每个微透镜后都会聚焦在一点,聚焦点的位置被能够反应出光束的方向,然后反推出光的波前信息。下面的内容是模拟光束经过透镜后聚焦的过程,然后简单的叙述了两种相位恢复的算法。

模拟步骤
1. 构建相位面,获取焦面上的图像,计算斜率
2. 重建波前方法分为两种,一种是区域法,一种是模型法。
3. 对比重构之后的相位和输入的相位面,对比结果
构建相位面,计算质心,获取斜率
1、构建相位面
数字化处理的方式多是无量纲的数据,因此默认量纲为a,假设为1um。
一个连续的光斑,光强和相位面是连续的,这里将它离散,变成一个二维矩阵,单个像素的大小为a。相位面经过微透镜阵列后聚焦到ccd阵列所在的平面,现在要知道相位面的方向和CCD上质心位置和光束方向(斜率)的关系。
补充:离散傅里叶变换公式
一维傅里叶变换

二维时序图
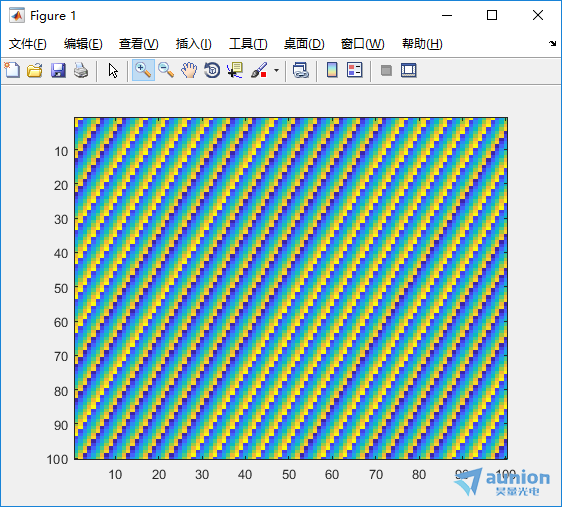
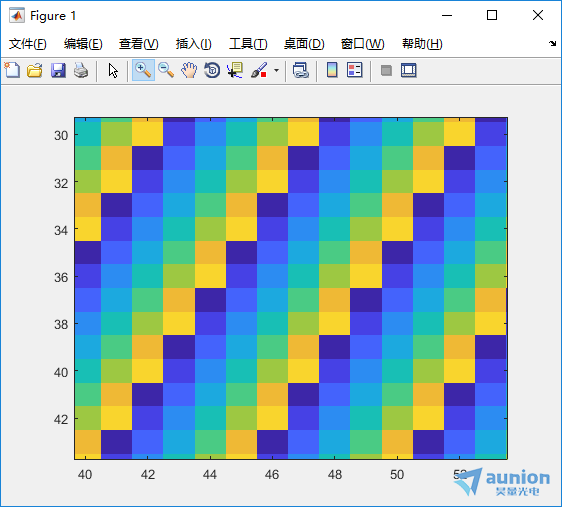
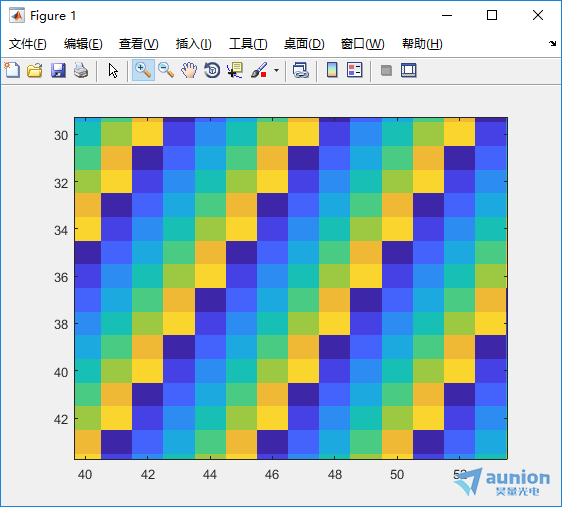


从上图可看到,顶峰的位置位于(21,11),振幅为1
从一维时序图可以猜测,(1,1)位置应该是直流偏量的值,需要将顶峰的位置各自减1处理后得到(20,10)在乘以最低频率0.01得到该顶峰对应的频率为0.2和0.1,与上述结果一致




从公式的角度看,2x/50=1得到x=25,因此x方向周期为25,频率0.04;3y/50=1得到y=16.67,频率为=0.06,最低频率1/512
傅里叶频谱

减1后得到坐标(20, 31),乘以最低频率=(0.039,0.060)
上图用于读取顶点的坐标比较方便,但是实际显示的效果应该图下图所示

对应坐标是(277, 288),与上图的区别在于是对坐标系做斜线交叉,使用的是fftshift函数,如果变成(21,32)需要减去坐标(256, 256),即中心坐标。
上边这些过程,讲述的是一个光斑,经过透镜后的傅里叶变化结果,也是它的光斑形状。
现在的问题是如何把傅里叶变换结果与实际光斑大小对应,然后根据焦距计算斜率
现在不知道透镜焦距的情况下,是否能根据现有的傅里叶变化结果计算光束的偏转角度
频谱对应的是周期,知道周期就能都知道光束的角度
知道光束方向,然后依据焦距,能够知道光斑的放大比例。
实际频率=最低频率*定点偏移量
周期=实际频率的倒数

由上述的表述,可以知道知道的结果是,由实际相位图->傅里叶变化频谱->依据焦距获取实际光斑大小
构造相位面:

1. 构造相位面
为了检验方便,先构造两个相差,选曲第三项和第四项



假设的相位图,z的形状如图所示,2对应4pi
将相位图划分成为5*5的透镜整列,每个透镜下面对应20*20的像素,假设焦距的放大比例正好是1,即傅里叶变换的结果即实际结果,最终想要的只是斜率,实际光斑的位置其实无关紧要。
傅里叶变换的结果,分辨率比较低,因此扩充函数,多余的项目填充0,例如第一个透镜对应20*20像素,扩充到300*300
![]()



获取不同图像下的结果,保存X和Y方向的斜率,以及光强图




对应的频率为:

补充:光斑质心计算
当对入射光进行傅里叶变换后,得到的光斑,过去是寻找光斑中最大值作为光斑的中心,这种方法效果不太理想,当相差级数越来越多的时候,还原的相位差距也越来越大。
因此将寻找最大值的方法改成寻找光斑质心,光斑相差不断增大的情况下,误差相对更小

输入光斑相差为10项,输入相差和重构之间的差别

输入光斑相差为20项,输入相差和重构之间的差别


从上图看,在15项之前,结果比较相近,之后不太稳定
区域法恢复波前
建立模型,然后重建波前,常见的模型有下面三种:




展示全部 
